Kalkulus
Contoh Soal :
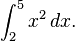
Di sini,

dan kita dapat menggunakan

sebagai antiturunan. Sehingga:
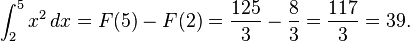
Atau lebih umumnya, misalkan kita perlu menghitung
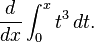
Di sini,
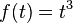
dan kita dapat menggunakan

sebagai antiturunan. Sehingga:
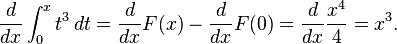
Namun hasil ini akan lebih mudah didapatkan apabila menggunakan:

Andaikan
Misalkan terdapat dua bilangan
x1 dan
x1 + Δ
x pada [
a,
b]. Sehingga didapatkan

dan
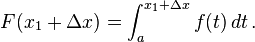
Pengurangan kedua persamaan di atas menghasilkan
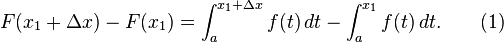
Bisa ditunjukan bahwa

- (Jumlah dari luas wilayah yang bersampingan sama dengan jumlah kedua wilayah yang digabungkan.)
Dengan memanipulasi persamaan ini, kita dapatkan
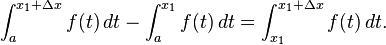
Substitusikan persamaan di atas ke (1), sehingga
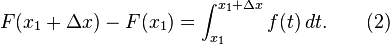
Menurut
teorema nilai antara untuk pengintegralan, terdapat sebuah
c pada [
x1,
x1 + Δ
x] sehingga
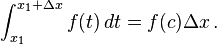
Substitusikan persamaan di atas ke (2), kita dapatkan

Bagi kedua sisi dengan Δ
x, menghasilkan
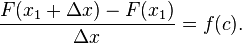
- Perhatikan pula ekspresi pada sisi kiri persamaannya adalah hasil bagi beda Newton untuk F pada x1.
Dengan mengambil limit Δ
x → 0 pada kedua sisi persamaan:
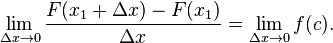
Ekspresi pada sisi kiri persamaan adalah definisi turunan dari
F pada
x1.

Untuk mencari limit lainnya, kita gunakan
teorema apit.
c ada pada interval [
x1,
x1 + Δ
x], sehingga
x1 ≤
c ≤
x1 + Δ
x.
Juga,
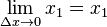
dan

Sehingga menurut teori apit,
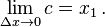
Substitusikan ke (3), kita dapatkan
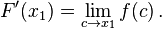
Fungsi
f kontinu pada
c, sehingga limit dapat diambil di dalam fungsi. Oleh karena itu, kita dapatkan
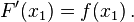
yang menyelesaikan pembuktian
Misalnya
f kontinu pada interval [
a,
b], dan
F adalah antiturunan dari
f. Dimulai dengan kuantitas

Misalkan pula terdapat bilangan-bilangan
- x1, ..., xn
sehingga

Maka

Sekarang kita tambahkan setiap
F(
xi) bersamaan dengan balikan aditif (
inverse additive), sehingga kuantitas yang dihasilkan adalah sama:
![\begin{matrix} F(b) - F(a) & = & F(x_n)\,+\,[-F(x_{n-1})\,+\,F(x_{n-1})]\,+\,\ldots\,+\,[-F(x_1) + F(x_1)]\,-\,F(x_0) \, \\
& = & [F(x_n)\,-\,F(x_{n-1})]\,+\,[F(x_{n-1})\,+\,\ldots\,-\,F(x_1)]\,+\,[F(x_1)\,-\,F(x_0)] \,. \end{matrix}](http://upload.wikimedia.org/math/b/d/e/bde262027624d2d1b7d79d67751f9444.png)
Kuantitas di atas dapat ditulis sebagai penjumalhan berikut:
![F(b) - F(a) = \sum_{i=1}^n \,[F(x_i) - F(x_{i-1})]\,. \qquad (1)](http://upload.wikimedia.org/math/5/f/b/5fbb95b91da8e3ddceb869337d7323d5.png)
Kemudan kita akan menggunakan
teorema nilai purata. Dinyatakan dengan singkat,
Misalkan
F kontinu pada interval tertutup [
a,
b] dan terdiferensialkan pada interval terbuka (
a,
b). Maka terdapat
c pada (
a,
b) yang

Sehingga

Fungsi
F terdiferensialkan pada interval [
a,
b]; sehingga ia juga terdiferensialkan dan kontinu pada setiap interval
xi-1. Oleh karena itu, menurut teorema nilai purata,
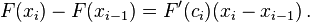
Substitusikan persamaan di atas ke (1), kita dapatkan
![F(b) - F(a) = \sum_{i=1}^n \,[F'(c_i)(x_i - x_{i-1})]\,.](http://upload.wikimedia.org/math/9/a/2/9a27d0ce017fd6a29ffc33d230617973.png)
Asumsi ini mengimplikasikan

Juga,

dapat diekspresikan sebagai

dari partisi

.
![F(b) - F(a) = \sum_{i=1}^n \,[f(c_i)(\Delta x_i)]\,. \qquad (2)](http://upload.wikimedia.org/math/2/3/7/2371fea52b0fcdf7735b3d7eb5c7ef11.png)

Deret yang konvergen dari penjumlahan Riemann. Angka pada kanan atas
adalah luas dari persegi panjang abu-abu. Ia konvergen ke intergal
fungsi tersebut.
Perhatikan bahwa kita sedang menjelaskan luas persegi panjang, dengan
lebar kali tinggi, dan kita menggabungkan total semua luas persegi
panjang tersebut. Setiap persegi panjang, dengan
teorema nilai purata, merupakan pendekatan dari bagian kurva yang digambar. Juga perhatikan bahwa

tidak perlulah sama untuk setiap nilai

,
atau dengan kata lain lebar persegi panjang dapat berbeda-beda. Apa
yang perlu kita lakukan adalah mendekatkan kurva tersebut dengan

persegi panjang. Semakin kecil partisi ini dan semakin besar n, maka
kita akan mendapatkan luas wilayah kurva yang semakin mendekati nilai
sebenarnya.
Dengan mengambil limit ekspresi norma partisi mendekati nol, kita mendapatkan
integral Riemann.
Yakni, kita mengambil limit partisi yang terbesar mendekati nol dalam
hal ukuran, sehingga partisi-partisi lainnya lebih kecil dan jumlah
partisi mendekati tak terhingga.
Maka kita mengambil limit pada kedua sisi (2). Kita dapatkan
![\lim_{\| \Delta \| \to 0} F(b) - F(a) = \lim_{\| \Delta \| \to 0} \sum_{i=1}^n \,[f(c_i)(\Delta x_i)]\,.](http://upload.wikimedia.org/math/2/9/1/291ffe044566ee45e9edf75a078f0a9e.png)
Baik
F(
b) maupuan
F(
a) tidak bergantung pada ||Δ||, sehingga limit pada bagian sisi kiri tetaplah
F(
b) -
F(
a).
![F(b) - F(a) = \lim_{\| \Delta \| \to 0} \sum_{i=1}^n \,[f(c_i)(\Delta x_i)]\,.](http://upload.wikimedia.org/math/c/5/7/c57e85d849c57c1ebd9f8c17a575c57b.png)
Ekspresi pada sisi kanan persamaan merupakan definisi dari integral terhadap
f dari
a ke
b. Sehingga kita dapatkan:
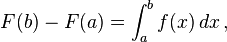
yang menyelesaikan pembuktian.
 dan kita dapat menggunakan
dan kita dapat menggunakan  sebagai antiturunan. Sehingga:
sebagai antiturunan. Sehingga: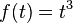 dan kita dapat menggunakan
dan kita dapat menggunakan  sebagai antiturunan. Sehingga:
sebagai antiturunan. Sehingga:
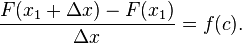
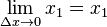 dan
dan 
 Juga,
Juga,  dapat diekspresikan sebagai
dapat diekspresikan sebagai  dari partisi
dari partisi  .
. tidak perlulah sama untuk setiap nilai
tidak perlulah sama untuk setiap nilai  ,
atau dengan kata lain lebar persegi panjang dapat berbeda-beda. Apa
yang perlu kita lakukan adalah mendekatkan kurva tersebut dengan
,
atau dengan kata lain lebar persegi panjang dapat berbeda-beda. Apa
yang perlu kita lakukan adalah mendekatkan kurva tersebut dengan  persegi panjang. Semakin kecil partisi ini dan semakin besar n, maka
kita akan mendapatkan luas wilayah kurva yang semakin mendekati nilai
sebenarnya.
persegi panjang. Semakin kecil partisi ini dan semakin besar n, maka
kita akan mendapatkan luas wilayah kurva yang semakin mendekati nilai
sebenarnya.
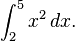
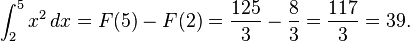
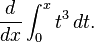
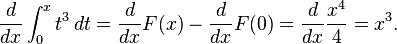



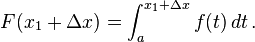
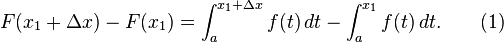
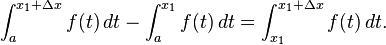
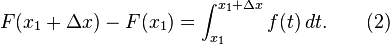
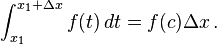

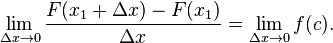

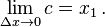
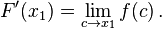
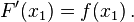



![\begin{matrix} F(b) - F(a) & = & F(x_n)\,+\,[-F(x_{n-1})\,+\,F(x_{n-1})]\,+\,\ldots\,+\,[-F(x_1) + F(x_1)]\,-\,F(x_0) \, \\
& = & [F(x_n)\,-\,F(x_{n-1})]\,+\,[F(x_{n-1})\,+\,\ldots\,-\,F(x_1)]\,+\,[F(x_1)\,-\,F(x_0)] \,. \end{matrix}](http://upload.wikimedia.org/math/b/d/e/bde262027624d2d1b7d79d67751f9444.png)
![F(b) - F(a) = \sum_{i=1}^n \,[F(x_i) - F(x_{i-1})]\,. \qquad (1)](http://upload.wikimedia.org/math/5/f/b/5fbb95b91da8e3ddceb869337d7323d5.png)


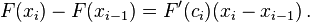
![F(b) - F(a) = \sum_{i=1}^n \,[F'(c_i)(x_i - x_{i-1})]\,.](http://upload.wikimedia.org/math/9/a/2/9a27d0ce017fd6a29ffc33d230617973.png)
![F(b) - F(a) = \sum_{i=1}^n \,[f(c_i)(\Delta x_i)]\,. \qquad (2)](http://upload.wikimedia.org/math/2/3/7/2371fea52b0fcdf7735b3d7eb5c7ef11.png)

![\lim_{\| \Delta \| \to 0} F(b) - F(a) = \lim_{\| \Delta \| \to 0} \sum_{i=1}^n \,[f(c_i)(\Delta x_i)]\,.](http://upload.wikimedia.org/math/2/9/1/291ffe044566ee45e9edf75a078f0a9e.png)
![F(b) - F(a) = \lim_{\| \Delta \| \to 0} \sum_{i=1}^n \,[f(c_i)(\Delta x_i)]\,.](http://upload.wikimedia.org/math/c/5/7/c57e85d849c57c1ebd9f8c17a575c57b.png)
Tidak ada komentar:
Posting Komentar