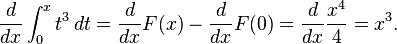Kalkulus
Contoh Soal :
 dan kita dapat menggunakan
dan kita dapat menggunakan  sebagai antiturunan. Sehingga:
sebagai antiturunan. Sehingga: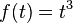 dan kita dapat menggunakan
dan kita dapat menggunakan  sebagai antiturunan. Sehingga:
sebagai antiturunan. Sehingga: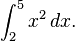
 dan kita dapat menggunakan
dan kita dapat menggunakan  sebagai antiturunan. Sehingga:
sebagai antiturunan. Sehingga: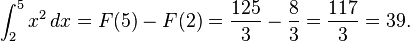
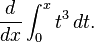
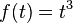 dan kita dapat menggunakan
dan kita dapat menggunakan  sebagai antiturunan. Sehingga:
sebagai antiturunan. Sehingga: